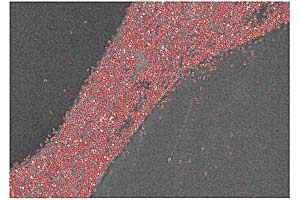
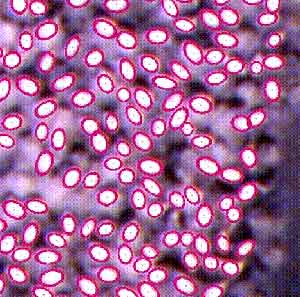
Стохастические алгоритмы для задач выделения некоторых характеристик изображений на основе гиббсовских непрерывных случайных полей и соответствующих стохастических динамик глауберова типа (рождения - гибели, смена марки) начали активно использоваться в теории обработки изображений сравнительно недавно. Прежде всего, эти алгоритмы хорошо адаптированы к задачам выделения объектов, имеющих сходную структуру, в случае детектирования деревьев или птиц объекты моделируются дисками или эллипсами,  для выделения зданий используется моделирование с помощью прямоугольников. Пиксельные модели для таких задач менее пригодны, т.к. описать геометрическую структуру выделяемых объектов с помощью какого-либо локального взаимодействия, характерного для пиксельных моделей, практически невозможно. 

     В работе [1] был разработан алгоритм, позволяющий автоматически решать задачу детектирования. В основе этого алгоритма лежит стохастическая равновесная динамика рождения-гибели в пространстве конфигураций в непрерывном пространстве, стационарная мера которой имеет гиббсовский вид, и в которой заложены все необходимые требования на искомую конфигурацию. Этот алгоритм представляет собой эволюцию макро-объектов, находящихся в непрерывном пространстве. Существенным отличием этого алгоритма от существующих в настоящее время стохастических алгоритмов для непрерывных моделей, таких как, например, RJMCMC (Random Jump Monte Carlo Markov Chain), является возможность за один итерационный шаг произвести кардинальное изменение текущей конфигурации, что приводит к значительному ускорению сходимости. Обзор существующих алгоритмов и сравнение с новым подходом можно найти в наших работах [2, 5].

     В нашей работе [1] была рассмотрена модель дисков, где каждый диск соответствовал выделяемому объекту, например, кроне дерева или очертанию птицы. Таким образом, задача алгоритма сводилась к нахождению конфигурации дисков, как можно лучше перекрывающихся с детектируемыми объектами и минимально перекрывающимися между собой. При этом нужно отметить, что границы реальных объектов на исходном изображении как правило нечеткие, с перекрытиями и сильно изрезанные. Опишем алгоритм более подробно. В основе предложенной схемы  лежит стохастическая динамика для модели точечного поля в непрерывном пространстве. Конфигурация точечного поля отождествляется с конфигурацией центров дисков фиксированного радиуса. Эта динамика представляет собой стохастический процесс рождения-гибели точек внутри некоторой ограниченной области непрерывного пространства, например, квадрата. При этом интенсивности рождения и гибели в общем случае зависят от текущей конфигурации дисков, а также от функции энергии. Выбор этих интенсивностей неоднозначен, и определяется так называемым условием детального баланса. В нашей схеме мы рассматриваем однородные по пространству интенсивности рождения и неоднородные интенсивности гибели. Таким образом строится равновесная динамика в непрерывном времени. Далее эта динамика подвергается специальной процедуре, называемой аннилингом. В результате этой процедуры с течением времени также меняется температура системы. При правильной скорости понижения температуры динамика должна стремиться к тем конфигурациям, на которых достигается глобальный минимум функции энергии. В численных расчетах мы использовали экспоненциальное убывание с малым показателем экспоненты, хотя из теоретических соображений убывание должно быть более медленным. Последним этапом построения алгоритма является дискретизация по времени построенной непрерывной динамики. При этом нами доказана сходимость этой дискретизации к непрерывному процессу. Дискретный по времени процесс представляет собой неоднородную марковскую цепь, и именно этот процесс и является основой нашего алгоритма.

     Выбор функции энергии – отдельная интересная проблема, так как в этой функции должна проявиться зависимость эволюции макро-объектов от данных. В наших исследованиях мы анализировали два различных выражения для функции энергии. Одно из них зависит от так называемого силуэта, т.е. объединения как множеств всех «живущих» в данный момент дисков. В этой модели хорошо выделялись объекты, располагающиеся в темной зоне, но в области светлого цвета, например, когда есть области полей, алгоритм расставляет на этих областях плотную упаковку дисков, считая, что эта область заполнена исследуемыми объектами. Поэтому этот выбор функции энергии хорош после предварительной обработки изображения (сегментации), а именно после выделения тех областей на изображении, которые содержат исследуемые объекты. Другое выражение для функции энергии более универсально, оно также хорошо работает в случае, когда на снимке есть большие светлые области, не заполненные объектами (например, поля). Эта функция учитывает не только внутренность диска, но также и граничную область, и при этом минимум энергии достигается в том случае, если на данных граница объекта хорошо контрастирует с внутренней областью. Так как для этой функции важен именно контраст между внутренностью и границей, в этой модели возникали некоторые трудности при выделении кроны близко расположенных друг к другу деревьев, т.е. в случае, когда происходит перекрытие дисков. Здесь важен правильный выбор параметров модели.

     Основной вывод, который был нами сделан, при анализе изображений с помощью предложенного алгоритма, - стохастическая схема для данного типа задач работает быстро и качественно, главным образом за счет новой идеи ввести динамику макро-объектов и возможности множественного изменения конфигурации за один итерационный шаг. При этом совершенно не важна общая структура объектов на фотографии (например, упорядоченность посадок при распознавании деревьев), алгоритм так же надежно работает при выделении хаотично расположенных птиц.

     Дальнейшее направление исследований связано с системами, содержащими макро-объекты с одним или более внутренними параметрами (степенями свободы), см. [3, 4]. Такие системы называются моделями маркированных точечных полей, а внутренние параметры объекта называются марками. Например, в случае динамики эллипсов, марками являются величины полуосей и ориентация эллипсов. При этом новая динамика помимо процесса рождения-гибели содержит диффузионную часть, отвечающую изменению этих марок. Здесь в зависимости от задачи возможно сочетание детерминированных и стохастических диффузионных динамик.

Литература

1. Descombes X., Minlos R.A., Zhizhina E., Object extraction using stochastic birth-and-death dynamics in continuum, Journal of
Mathematical Imaging and Vision, Vol.33 (3), p. 347, 2009.
2. Descombes X., Zhizhina E., The Gibbs fields approach and related dynamics in image processing, Condensed Matter Physics, 2008, Vol. 11, No.2, p. 1-20.
3. M. Kulikova, I. Jermyn, X. Descombes, J. Zerubia, E. Zhizhina, Extraction of arbitrarily shaped objects using stochastic multiple birth-and-death dynamics and active contours, IS&T/SPIE Electronic Imaging 2010 meeting, 17-21 January 2010, San Jose, California, USA.
4. M. Kulikova, I. Jermyn, X. Descombes, J. Zerubia, E. Zhizhina, A marked point process model with strong prior shape information for the extraction of multiple, arbitrarily-shaped objects, SITIS, The 5-th International Conference on Signal-Image Technology & Internet-based Systems, November 29- December 4, 2009, Marrakech.
5. E. Zhizhina, X. Descombes, Gibbs point field models for extraction problems in image analysis, Proceedings of Dobrushin International Conference, Moscow, Russia, July 15-20 2009, ISBN 978-5-901158-10-4.